Lesson notes :

NOTE : The sum query function is a constant one which means that it always gives us a constant sensitivity, for our case we have a binary db, by removing one person i.e removing a 0 or 1, our maximum distance between the full db and a parallel_db aka sensitivity, can only be = 1. **

Sensitivity : The maximum amount that the query changes when removing an individual from the database, also called the L1 Sensitivity.

Assignment 2 : Evaluating the Privacy of a Function

My solution :

# try this project here!
def query_mean(db):
    return torch.mean(db.type(torch.float64))

def sensitivity(query, num_entries):
    db, pdbs = create_db_and_parallels(num_entries)
    sensitivity = 0 
    full_db_result = query(db)
    for pdb in pdbs:
        pdb_result = query(pdb)

        db_distance = torch.abs(full_db_result - pdb_result)

        if(db_distance > sensitivity):
            sensitivity = db_distance

    return sensitivity

sensitivity(query_mean, 5000)

Assignment 3 : Calculate L1 Sensitivity For Threshold

My solution :

# try this project here!
def treshold_func(db):
    threshold = 5
    if(query(db) > threshold):
        return 1 
    else:
        return 0
for i in range(10):
    print(f"Sensitivity {i} : {sensitivity(treshold_func, 10)}")

NOTE : the intuition we can get from these results are for Sensitivity with the value of 0 , we could say that by removing an individual (labeled 0/1) the output of our query didn't change (i.e. if the sum was ≤ 5 or was > 6). For Sensitivity with the value of 1, here the sum of our db must be == 6 , so that by removing an individual labeled as (1) our query output will change thus having a 1 sensitivity.

Assignment 4 : Perform a Differencing Attack on Row 10

My solution :

# try this project here!
#using the sum query
db, pdbs = create_db_and_parallels(10)
print(f'The value of the person in row 10 : {query(db) - query(pdbs[9])}')
print(f'The real value from db is : {db[9]}')
#using the treshold query
print(f'The value of the person in row 10 : {(query(db) > (db.sum()-1)).float() - (query(pdbs[9]) > (db.sum()-1)).float()}')

Introducing Local and Global Differential Privacy

Introduction : To protect the data from malicious attacks, we tend to add random noise to the database and to the queries in the db, there's two types of differential privacy, Local DP where we add noise directly to the db or having individuals adding noise to their data, the other type is called Global DP where noise is added on the output of the query, this last one needs the data operator to be trustworthy.

Difference : If the data operator is trustworthy then the only difference is that we can achieve better result with Global DP, with same level of privacy. In the Differential Privacy literature the database owner is called Trusted Curator.

1 - Local Differential Privacy :

Given a collections of individuals , each individual will add random noise to his data before sending it to the statistical database, thus the protection is happening at a local level.

• Differential Privacy always requires some form of noise or randomness applied to the query to protect the database from differenting attacks.

Randomized Response : Technique used in social sciences when trying to learn about the high level trends for a taboo behavior.

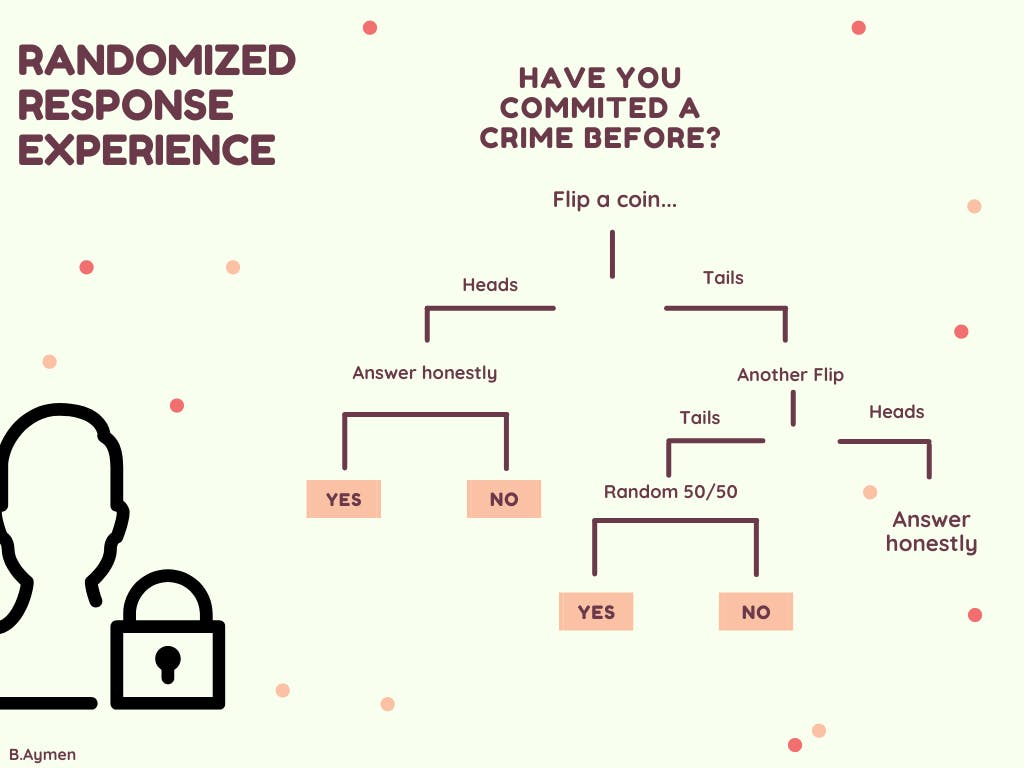
Randomized Response experience

We have gained privacy here but we have lost on accuracy specially if we are sampling over a small amount of people. this trend is true through all the field of DP, thus we can distinguish two main research themes :

• Most accurate query with the greatest amount of privacy
• Greatest fit with trust models in the actual world ( by that we mean that if we keep preserving privacy between two parties who trust each other then we've lost accuracy for nothing), we are talking here about flexible models.

Assignment 4: Randomized Response (Local Differential Privacy)

My solution :

from random import random
# try this project here!
#implementing randomized response 
def randomized_response(size):
    db, _ = create_db_and_parallels(size)
    #coin flip -> HEADS == 1 , TAILS == 0 / YES == 1 , NO == 0
    db_noised = db.detach().clone() 
    coin_flip1 = (torch.rand(size) > 0.5).type(torch.uint8)
    coin_flip2 = (torch.rand(size) > 0.5).type(torch.uint8)
    db_noised = db * coin_flip1 +(1-coin_flip1)*coin_flip2
    return db, db_noised

db, db_noised = randomized_response(10)
print(f'db before noise : {db}')
print(f'db after noise: {db_noised}')

#query db 
print(query_mean(db))
print(query_mean(db_noised))

sizes = [10 , 100, 1000, 10000]
for size in sizes: 
    db, db_noised = randomized_response(size)
    print(f'size : {size}')
    print(f'db before noise : {query_mean(db)}')
    print(f'db after noise: {query_mean(db_noised)*2-0.5}')

NOTE : as we can notice here, for a large db size the difference between non-noised db and noised db becomes very small thus for very large databases applying local DP will not affect our statistical analyses that much. **

Assignment 5 : Project: Varying Amounts of Noise

My solution:

# try this project here!
#implementing randomized response 
def randomized_response_biased(size, bias):
    db, _ = create_db_and_parallels(size)
    #coin flip -> HEADS == 1 , TAILS == 0 / YES == 1 , NO == 0
    db_noised = db.detach().clone() 
    coin_flip1 = (torch.rand(size) > bias).type(torch.uint8)
    coin_flip2 = (torch.rand(size) > 0.5).type(torch.uint8)
    db_noised = db * coin_flip1 +(1-coin_flip1)*coin_flip2
    return db, db_noised

db, db_noised = randomized_response_biased(10, 0.7)
print(f'db before noise : {db}')
print(f'db after noise: {db_noised}')

sizes = [10, 100, 1000, 10000]
for size in sizes: 
    bias = 0.7
    db, db_noised = randomized_response_biased(size, bias)
    print(f'size : {size}')
    print(f'db before noise : {query_mean(db)}')
    query = query_mean(db_noised)
    print(f'db after noise: {(query - (1-bias)*0.5)/bias}')
    print(f'db after noiseV2: {((query/bias) - 0.5) * bias/(1-bias)}')

Creating a Differentially Private Query

• epsilon could be interpreted as the amount of information leakage that we want to allow.
• delta is the probability of surpassing the amount of information leakage defined by epsilon.

Randomized mechanism : A function with random noise added to its inputs, outputs and/or inner workings.

NOTE: Laplacian noise has a particularity of having a delta == 0 which means that the probability of surpassing epsilon is zero.

My solution for this :

import numpy as np
epsilon = 0.5
db, pdbs = create_db_and_parallels(100)
def laplacian_noise(query, epsilon):
    b = sensitivity(db, pdbs, query) / epsilon ; 
    noise = torch.Tensor(np.random.laplace(0, b, 1)); 
    return query(db) + noise

laplacian_noise(query_sum, epsilon)
laplacian_noise(query_mean, epsilon)